คำศัพท์และสัญลักษณ์ของเซต[แก้]
- เราอาจจะคิดว่าเซต คือ กลุ่มของสิ่งต่างๆซึ่งมีกฎเกณฑ์ชัดเจนว่าสิ่งใดอยู่ในเซตและสิ่งใดไม่ได้อยู่ในเซต สิ่งที่อยู่ในเซตเรียกว่าสมาชิกของเซต โดยทั่วไปจะแทนเซตด้วยตัวอักษรภาษาอังกฤษตัวพิมพ์ใหญ่ เช่น A,B,C และแทนสมาชิกของเซตซึ่งยังไม่เจาะจงว่าคือตัวอะไรด้วยอักษรภาษาอังกฤษตัวพิมพ์เล็ก เช่น a,b,c
- วิธีเขียนเซต มีอยู่ 3 แบบ
- แบบข้อความ อธิบายเซตด้วยถ้อยคำ
- แบบแจกแจงสมาชิก เขียนสมาชิกทั้งหมดภายใต้ปีกกา {} และใช้จุลภาคคั่งระหว่างคู่
- แบบบอกเงื่อนไขของสมาชิก เขียนเซตในรูปแบบ {x | เงื่อนไขของ x}
- สมาชิกของเซตเป็นจำนวนหรือสิ่งใดก็ได้ เป็นเซตก็ได้
- เซตที่เท่ากัน เซตจะแตกต่างกันหรือไม่ขึ้นอยู่กับว่าสมาชิกต่างกันหรือไม่ โดยเซตสองเซตจะเท่ากันเมื่อมีสมาชิกเหมือนกัน
- เซตจำกัดและเซตอนันต์ เซตจำกัดคือเซตที่เราสามารถระบุได้ว่ามีสมาชิกกี่ตัว เซตอนันต์คือเซตที่ไม่ใช่เซตจำกัด
- เซตว่างคือเซตที่ไม่มีสมาชิกเลย
- เอกภพสัมพันธ์ คือเซตที่ใช้กำหนดขอบเขตของสิ่งที่กำลังพิจารณา แทนด้วย U
- เซตของจำนวนบางชนิด เช่น N = เซตของจำนวนนับ, I = เซตของจำนวนเต็ม, Q = เซตของจำนวนตรรกยะ, R = เซตของจำนวนจริง, C = เซตของจำนวนเชิงซ้อน
- สับเซต A เป็นสับเซตของ B หมายความว่าสมาชิกทุกตัวของ A เป็นสมาชิกของ B
- เพาเวอร์เซต ของ A คือเซตที่ประกอบด้วยสับเซตทั้งหมดของ A เขียนแทนโดย P(A)
การดำเนินการของเซต[แก้]
- ยูเนียน ของ A และ B คือเซตที่เกิดจากการรวบรวมสมาชิกของ A และ B เข้าไว้ด้วยกัน
- อินเตอร์เซกชัน ของ A และ B คือเซตที่ประกอบด้วยสมาชิกที่เหมือนกันของ A และ B
- ผลต่าง A – B คือเซตที่ประกอบด้วยสมาชิกของ A ที่ไม่ใช่สมาชิกของ B
- คอมพลีเมนต์ ของ A เขียนแทนด้วย A’ คือสับเซตของ U ที่ประกอบด้วยสมาชิกที่ไม่อยู่ ใน A
การนับจำนวนสมาชิกของเซต[แก้]
- ถ้า A เป็นเซตจำกัด เราใช้สัญลักษณ์ n(A) หรือ |A| แทนจำนวนสมาชิกของ A
- การนับจำนวนสมาชิกของ U ที่ไม่อยู่ใน A อาจใช้สูตร n(A’) = n(U)-n(A)
สมบัติของเซตที่ควรทราบ[แก้]
ให้ A, B, C เป็นเซตย่อยของเอกภพสัมพันธ์ U สมบัติต่อไปนี้จะเป็นจริง
- กฎการสลับที่
- กฎการเปลี่ยนกลุ่ม
- กฎการแจกแจง
- กฎการเอกลักษณ์


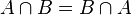



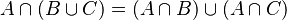

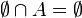
ไม่มีความคิดเห็น:
แสดงความคิดเห็น